Les distances dans le Système solaire
Forme et dimension de la Terre - Distance Terre-Lune
Premiers arguments
Malgré la curiosité cosmologique que suscite le ciel, l'idée que c'est celui-ci qui tourne autour de la Terre Terre
Terre
Minuscule fragment de matière flottant autour d'une étoile banale, la planète Terre est pourtant la plus massive des planètes telluriques.
Planète Terre restera longtemps gravée dans les esprits. Cependant, la rotondité de la Terre est un fait acquis depuis la plus haute Antiquité. Mais cette conception sera interdite par l'Église pour qui, selon l'interprétation des Écritures, la Terre ne pouvait être que rectangulaire et plane. Elle ne reconnaîtra son erreur qu'au XIIIe siècle.
Platon (427-347 av. J.-C.) imagine un UniversUnivers : ensemble de tout ce qui existe.
Glossaire sphérique dont la Terre occupe le centre.
Aristote (384-322 av. J.-C.) apporte quelques arguments pour étayer l'idée d'une Terre sphérique :
- les navires semblent s'enfoncer dans les flots à l'approche de l'horizonHorizon : projection sur la sphère céleste du plan horizontal passant par le point de vision de l'observateur.
Glossaire ; - l'ombre circulaire de la Terre sur son satellite lors des éclipses de Lune
 Lune
Lune
Le couple Terre-Lune peut être considéré comme une planète double qui orbite autour du Soleil à partir d'un centre de gravité commun…
Lune ; - de nouvelles étoilesÉtoile : elle se forme à partir d'un nuage de gaz qui s'effondre sous l'effet de la gravitation. Si la masse du nuage est suffisamment importante, la concentration de la partie centrale peut atteindre les conditions nécessaires aux réactions thermonucléaires.
Glossaire apparaissent lorsqu'on se déplace vers le Sud.
La forme de la Terre
Ératosthène (275-195 av. J.-C.), bibliothécaire à Alexandrie, considère que la Terre est ronde alors que la perception commune donne l'apparence du contraire.
Il imagina donc que si la lumière du Soleil Soleil
Soleil
Le Soleil n'est que l'une des 100 milliards d'étoiles qui constituent notre Galaxie.
Étoile Soleil atteint la Terre par la projection de rayons parallèles, il y avait deux possibilités :
- la Terre est plate et la lumière solaire provenant du zénithZénith : point de projection sur la voûte céleste de la droite partant du centre de la Terre et passant à l'aplomb d'un lieu, soit à 90° de hauteur au-dessus de l'horizon.
Glossaire ne produit aucune ombre quelque soit l'endroit où l'on se trouve ; - la Terre est ronde et les rayons solaires projettent des ombres de longueurs différentes suivant les lieux d'observations.
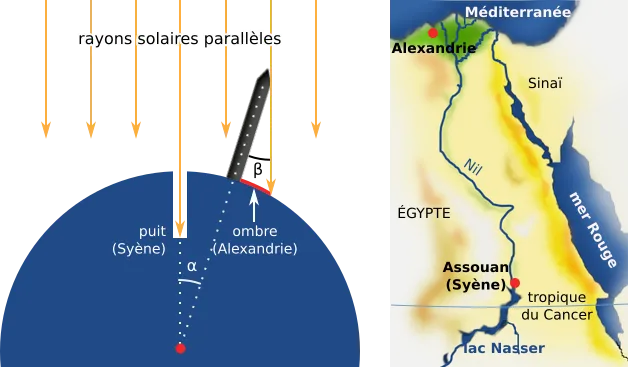
L'expérience d'Ératosthène
La ville de Syène (aujourd'hui Assouan) est située proche du tropique du Cancer. Ératosthène se fit rapporter que la lumière du Soleil y tombe d'aplomb, sans former d'ombre, au fond d'un puit au solsticeSolstice : en raison de l'inclinaison de l'axe de rotation terrestre sur le plan de son orbite, ce dernier n'est pas confondu avec l'équateur. Le Soleil passe ainsi par une déclinaison maximale deux fois par année. À ces points extrêmes, la position du Soleil semble s'arrêter pour reprendre une marche à rebours (sol stat, qui a donné solstitia).
Glossaire d'été. À cette même date, il mesure que l'ombre de l'obélisque d'Alexandrie forme un angle valant 1/50 de cercle (α = β = 1/50 de cercle).
Estimant la distance entre ces deux villes très légèrement supérieure à 5 000 stades (le stade, selon une valeur communément admise, valait 157,5 m) il parvint ainsi à estimer la circonférence de la Terre avec une précision remarquable : 39 375 km (pour une valeur équatoriale réelle de 40 075,02 km).
Dans son utilisation d'une méthode géométrique aussi graphique que géniale, la chance a servi Ératosthène car ses mesures étaient doublement erronées : Alexandrie et Syène ne sont pas situées sur le même méridien, de plus 5 346 stades les séparent et non 5 000. Par un heureux hasard, ces deux erreurs se corrigent et s'annulent. Mais l'idée d'associer la géométrie à l'astronomie a pris son chemin.
Premier arpentage
Aristarque de Samos (310-230 av. J.-C.), en proposant – avec 17 siècles d'avance sur Nicolas Copernic Nicolas Copernic
Nicolas Copernic
Après avoir étudié les mathématiques, la philosophie aristotélicienne et l'astronomie à l'université de Cracovie, il devient chanoine de Frauenburg en 1501, après un périple de trois années en Italie et un bref passage à l'université de Padoue…
Glossaire (1473-1543) ! – un système héliocentriqueHéliocentrisme : modèle cosmologique qui place le Soleil au centre de l'Univers.
Glossaire, tente une première estimation des distances relatives de la Lune et du Soleil à la Terre.
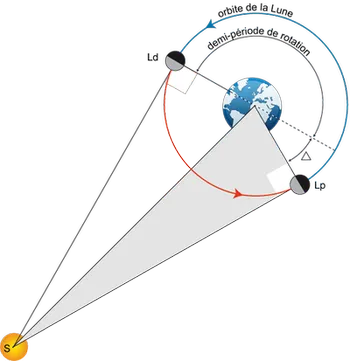
La Lune au Premier Quartier ou au Dernier Quartier montre, vue depuis la Terre, la moitié de sa face éclairée et la moitié de sa face non-éclairée… à ne pas confondre avec la face cachée qui est le côté en permanence opposé à la Terre ! Dans ces deux cas, l'axe Soleil-Lune est donc dans une direction perpendiculaire à celui de Terre-Lune.
Il présume que la Lune tourne autour de la Terre à vitesse constante sur une orbite circulaire.
De même, il suppose que le Soleil étant à une distance « finie », les positions de la Lune au Premier Quartier et Dernier Quartier ne sont pas diamétralement opposées.
L'écart entre la demi-période de rotation et le temps mis par la Lune pour passer d'un Premier Quartier (Lp) au Dernier Quartier (Ld) permet d'évaluer l'angle Δ (on suppose le mouvement de la Lune parfaitement circulaire et uniforme).
Par une démonstration géométrique graphique, on en déduit la distance Soleil-Terre (S-T) en fonction du rayon de l'orbite lunaire T-Lp dans le triangle rectangle T-Lp-S.
Le Soleil étant très éloigné, l'angle Δ est très petit et reste bien inférieur à la précision avec laquelle on détermine l'instant exact d'un Premier Quartier et Dernier Quartier.
À partir de cette méthode, et malgré toute son ingéniosité, Aristarque ne parvint à déduire que le Soleil était entre 18 et 20 fois plus éloigné que la Lune. Il avait trouvé un angle Δ égal à 12 h, alors qu'il n'est que de 35 min.
C'est pourtant cette valeur, erronée d'un facteur 20 (dans la réalité TS est égal à 400 fois le rayon de l'orbite lunaire), qui sera acceptée durant les 1 500 années suivantes.
Rapport Lune/Terre et géométrie
Aristarque émet l'hypothèse que l'ombre de la Terre pouvait être considérée comme un cylindre jusqu'à la distance de l'orbite de la Lune. Lors d'une éclipse centrale – à ce moment la Lune se trouve sur le plan de l'écliptiqueÉcliptique : projection du plan de l'orbite terrestre sur la voûte céleste. Pour cette raison, il correspond également au déplacement apparent du Soleil parmi les étoiles sur une année.
Glossaire et, passant par le centre de l'ombre de la Terre, la durée de l'éclipse est maximale – la Lune reste environ 2 heures dans la zone d'ombre. Se déplaçant d'une distance égale à son diamètre apparent en une heure, il calcule que le diamètre lunaire vaut ⅓ de celui de la Terre :
- la Lune entre dans l'ombre de la Terre ;
- une heure s'est écoulée, la Lune est entièrement éclipsée ;
- une première heure dans l'ombre et la Lune s'est déplacée d'un diamètre ;
- après deux heures d'éclipse, la Lune sort de l'ombre.
Avec une mauvaise estimation du diamètre de la Lune, la détermination de la distance Terre-Lune est également faussée.

Hipparque (190-125 av. J.-C.), avec une meilleure dimension du cône d'ombre estima cette distance à 38 fois le diamètre de la Terre.
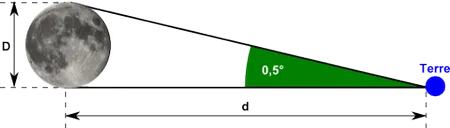
En réalité, l'ombre de la Terre forme un cône d'angle 0,5°, ce qui donne un diamètre lunaire égal à 0,27 fois celui de la Terre. La distance Terre-Lune devient alors égale à 30 diamètres terrestres.
Aristarque semble également avoir par la suite réévalué son diamètre lunaire. Fixant la période de révolution de la Lune à 29 jours, son déplacement horaire (donc son diamètre) correspond à 360 ÷ (29 × 24), soit ± 0,5°.
La distance d de la Lune vaut alors : D / tg 0,5°.
Parallaxe et radar
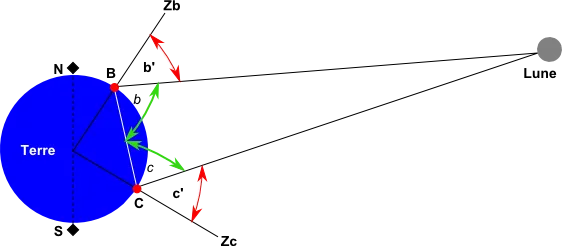
En 1751, une expérience menée depuis Berlin en B par Joseph Lefrançois de Lalande Joseph Lefrançois de Lalande
Joseph Lefrançois de Lalande
Directeur de l'observatoire de Paris, entre 1795 et 1800, il s'illustra également comme vulgarisateur en organisant des séances d'observations publiques…
Glossaire (1732-1807) et le cap de Bonne Espérance (ces deux lieux sont pratiquement sur un même méridien) en C par Nicolas-Louis de Lacaille Nicolas-Louis de Lacaille
Nicolas-Louis de Lacaille
Nicolas-Louis de Lacaille consacra une partie essentielle de sa vie à l'astronomie. En 1739, il participe à la mesure de la méridienne de France et entre deux ans plus tard à l'Académie des sciences. Entre octobre 1750 et juin 1754, il se retrouve au Cap pour mesurer l'arc du méridien…
Glossaire (1713-1762) permet de déterminer cette distance par la méthode des parallaxesParallaxe : regardée alternativement avec chaque œil, la projection du pouce, main tendue, ne se retrouve pas devant les mêmes éléments d'un décor : c'est l'effet de parallaxe. La parallaxe est d'autant plus petite que l'objet visé est lointain.
Glossaire.
Ils mesurent chacun l'angle séparant leur zénithZénith : point de projection sur la voûte céleste de la droite partant du centre de la Terre et passant à l'aplomb d'un lieu, soit à 90° de hauteur au-dessus de l'horizon.
Glossaire (Zb et Zc) au centre du disque lunaire lors d'un passage au méridien (soit b' et c'). La distance BC étant connue, il est possible de calculer les angles b et c. La distance Terre-Lune est déterminée par résolution du triangle B-Lune-C.
Aujourd'hui, à l'aide de signaux radar, il est possible de connaître cette distance avec une grande précision : quelques centimètres ! L'orbite de la Lune étant une ellipse, la distance est de 356 400 km au périgéePérigée : distance minimale d'un corps en orbite autour de la Terre.
Glossaire et portée à 406 700 km à l'apogéeApogée : distance maximale d'un corps en orbite autour de la Terre.
Glossaire, pour une distance moyenne de 384 401 km.